3D Morphable Models

#dl #ml #computer #vision #image #processing #face #recognition #deep-fakes

20200825140617

---

In computer vision it is really important to estimate the 3D shape of a head (face) from a single imeage, so as to create a 3D representation of that person.

The standard way of achieving this is thrgough a process that is called 3DMM, shorthand for 3D Morphable Models.

This is usefull for several topics, one of them being the need to detect faces of people from an image( [[20200815172158]] Detecting faces from images). The current state of the art (SoTA) on face detection is #retinaface with trains a NN for predicting multiple things all at once (face/noface, position, etc..) one of which is the orientation of the detected face. This is accomplished by using a 3DMM.

The way you would find the 3D structure of a person from a single image, is have a standard face model, modeled as a mesh of points (a triangulised surface) and then try to fit that to the given image. This is to say, get the 3D mesh and change it (morph it) in such a way as to end up with a 2D projection (image) really similar to what you have.

The PCA method (seminal paper)

Initially, this idea of morphing (how would you do this), started out from the core concept of isolating the core parts of a face (features) that could change from a face to another one. In other words, you were trying so see that you had:

• the forehead in a certain range (normalized to [0, 1] )
• the chin in a certain range (normalized to [0, 1] )
• eye size in a certain range (normalized to [0, 1])
• etc..

Finding these features was accomplished up to 2015 by using #pca (principal component analisys) on some 3D dataset of heads (e.g. CyberwareTM scans). By doing this you basically ended up with a 1D vector representation of each face, where the value of a single feature told you how far away (deformed) from the average mesh face you were on that specific feature (i.e. pca_face[2] = 0.73 that meant the feature 2 with corresponted to, let’s say, the forehead, had the value of 0.73).

To find the 1D vector that corresponds to a specific face, you first need to (manually) allign the template 3D face mesh over the target image (to make sure you have the correct rotation, orientation, azimuth, etc..) and then an optimisation process will try to tune the values of the initial 1D representation of the template 3D face mesh so as to minimize the RMSE between the target image and the 2D projection of the face mesh.

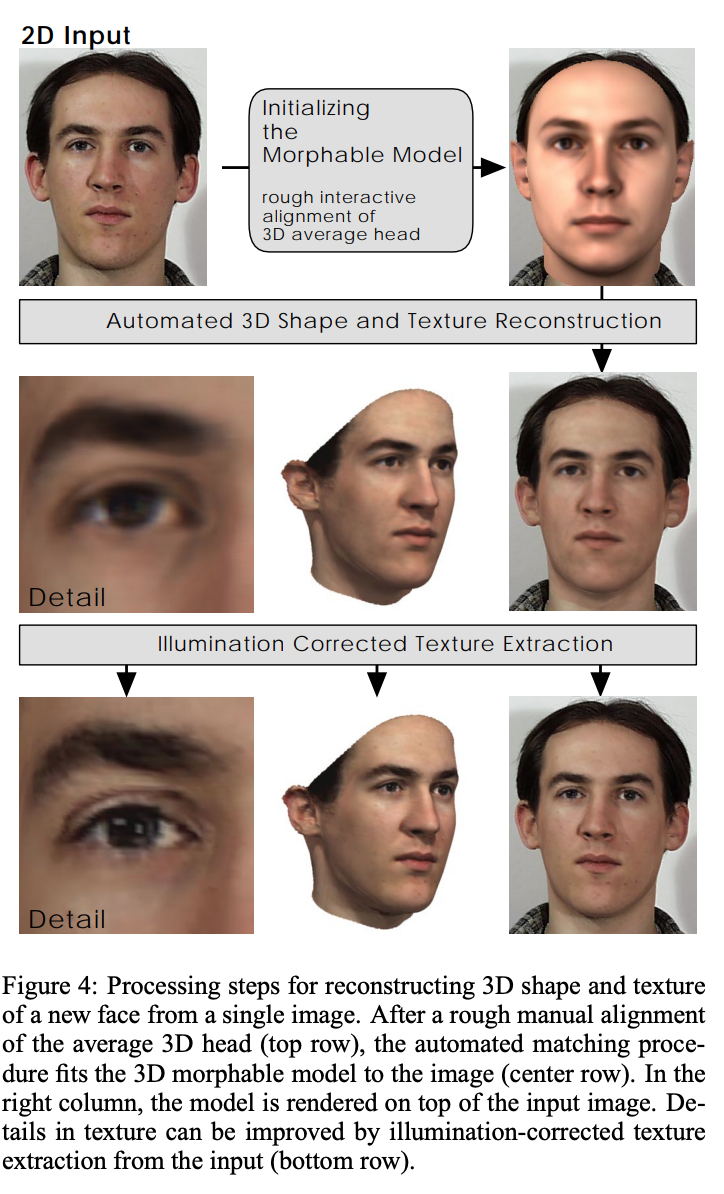Side Note: You actually represented a single face by two 1D vectors $S$ and $T$ that represented shape and texture (face color) respectively.

Having this representation, of being able to descirbe a face by a 1D vectors of values, you only need to find that 1D vector that morphed the model face mesh into a 3D face that, when projected on a 2D surface (like when a picture was taken) would be close to the original image.

Af course the position of the face should be known in order to make the correct 2D projection work, so this wasnt end-to-end and was improved by other approaches.

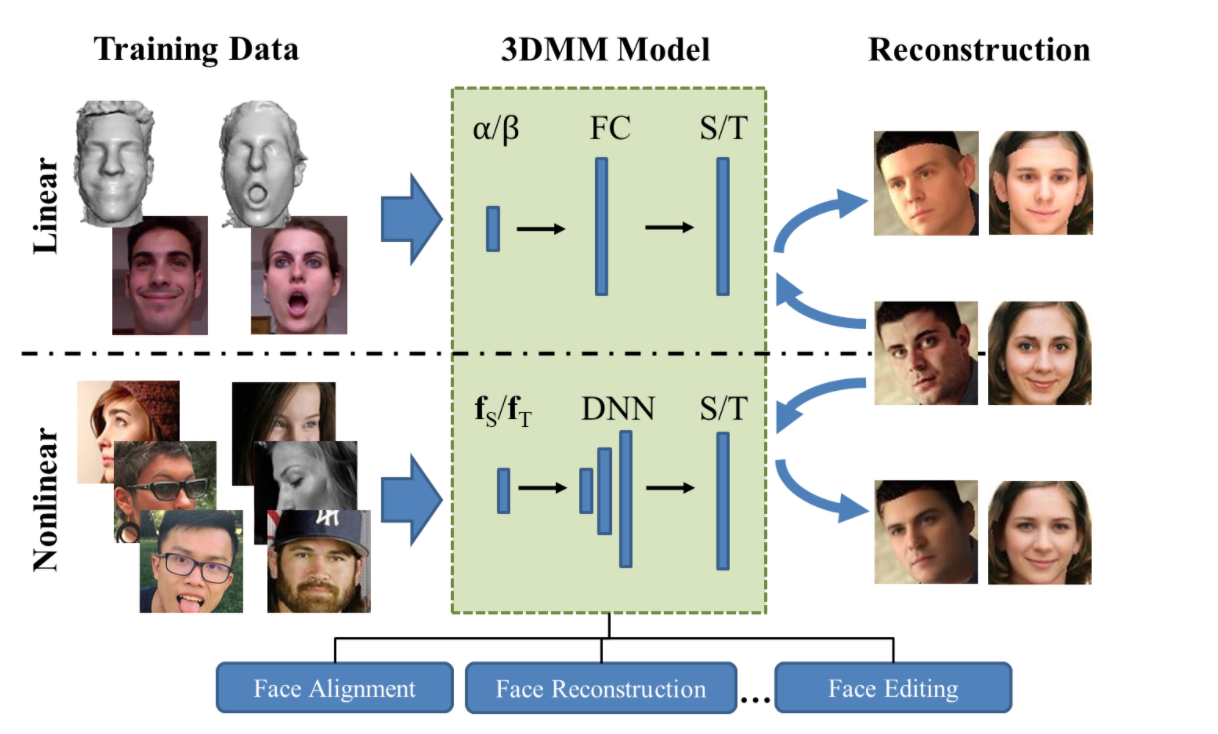
Nonlinear 3D Face Morphable Model

For the first approach to work you needed large datasets of 3D scans (for factoring out the PCA components of $S$ and $T$) and also the original images for the persons that these scans were taken from.

You also needed to manually allign (fixing the 3D projection) of the face before fitting any single face.

You also were limited by the linear nature of PCA, which restricted in what types of features you could extract (and model).

This new approach (2019) introduced a non-linear (aka NN based) approached the didn’t need 3D scans, was trained solely on 2D images and solved at the same time both the projection, the shape and the texture of the face of an input image.

This is a video demo of the paper and goes a long way of explaining the relation between 3DMMs and #deep-fakes. They also provide a GitHub repo with the working code.

Dense 3D Face Decoding over 2500FPS: Joint Texture & Shape Convolutional Mesh Decoders

Is a high performance / real-time (2500fps) 3DMM face decoder that uses CNN layers in the NN implemented in the above paper in order to achieve faster training in inference time.

This paper is also the one used while training #retinaface ([[20200903232600]] RetinaFace) and is published by the same authors of both #retinaface and #arcface, the ones behind the insightface.ai startup.

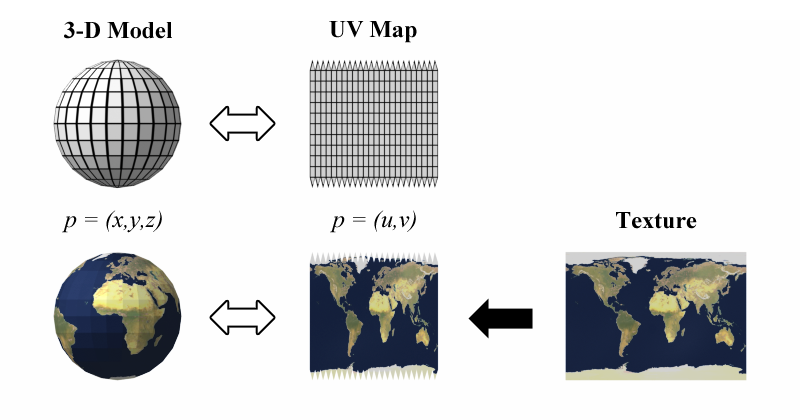
Among other things, they mention that they encode the face texture as a UV map which is a way to map / unmap a 3D object into a 2D surface, origami style.

Unsupervised Training for 3D Morphable Model Regression

This is a work published by Google in the 2018 paper titled “Unsupervised Training for 3D Morphable Model Regression”, where they present an end-to-end network that can learn unsupervised 3D faces from images. This paper presents an auto-encoder architecture, which takes and image, converts it to an embedding (via FaceNet or #vgg-face), then pass that embedding to a 3DMM decoder that outputs a 3D image, feed that 3D image in the differentible renderer to get a 2D image (projection) which is compared (via a loss function - this bit simplifying things) to the initial image, and the errors are backpropagated on the full architecture. So we have:

• FaceNet(Target 2D Image) => #face-embedding
• 3DMM(Face-Embedding) => 3D object
• Renderer(3D object) => Predicted 2D Image
• Loss(Target 2D Image, Predicted 2D Image)

The Renderer needs to be differentiable in order to for this system to be an end-to-end trainable one (all the pieces need to be differentiable).

The authors of #retinanet reused only the Renderer to incorporate it into their network, because they replace Google’s 3DMM step, with one based on the mesh convolutions (via graph convolutions). The basic idea though is that this step takes an input image and outputs a tuple $(S, T, P, I)$ for shape, texture, pose, illumination which is then decoded into a 2D image via Google’s renderer.

Google’s 3DMM decoder uses a 2-layer NN to transform the embeddings into s and t parameters that can be fed into the Basel Face Model 2017 3DMM. This makes Google’s approach really specific to faces, while (I believe) that the mesh convolutions approach can be applyed to any known regular object (like #books) as long as you can map them to a class of 3D morphable objects.

3DDFA_V2

A really recent paper that shows how to find landmarks on an image was published here. This is uses a 3DMM.