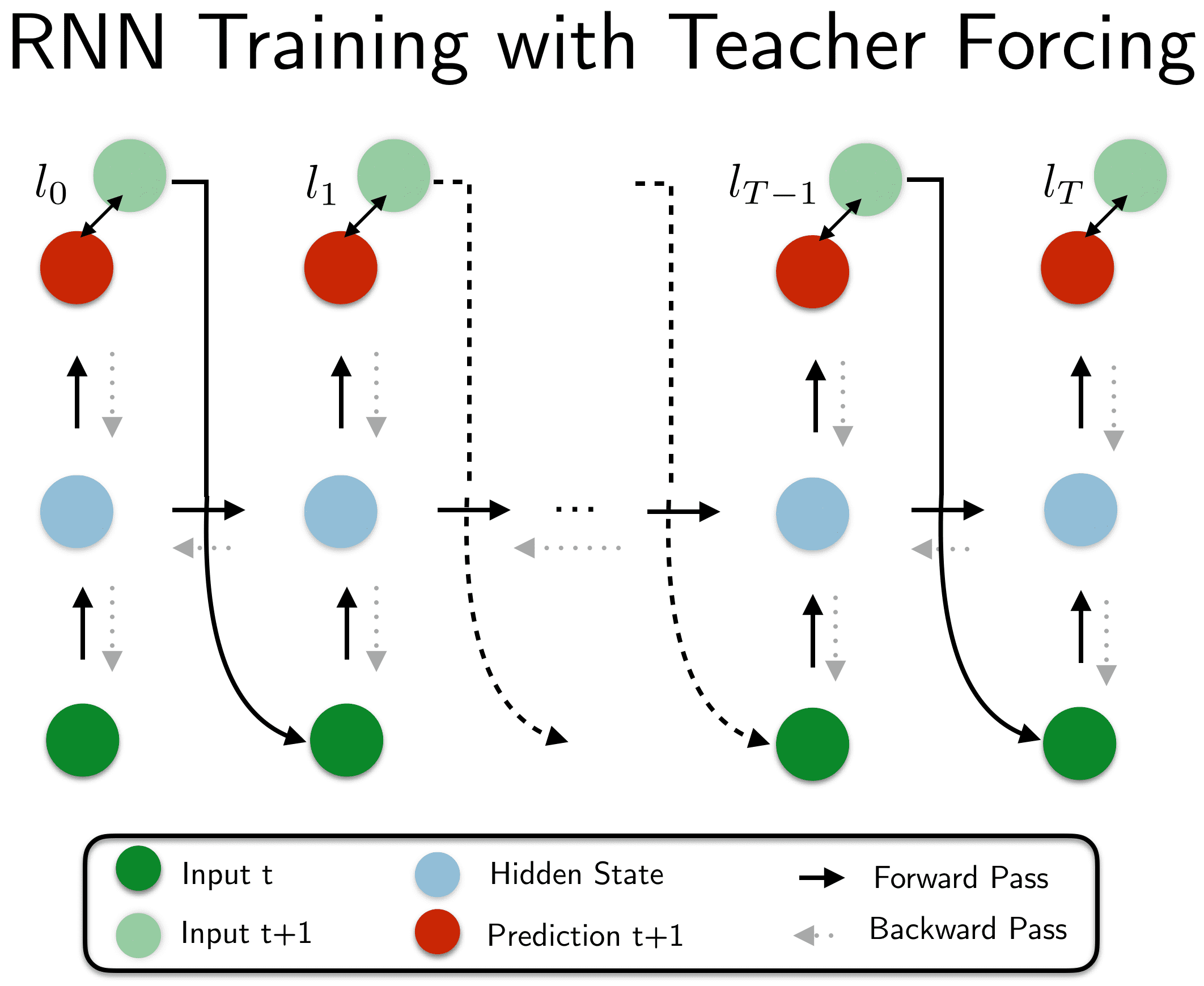
Training an RNN with teacher forcing.

#ml #dl #nlp

20200608182759

---

Teacher forcing is a (really simple) way of #training an #rnn.

RNNs have a variable length input and this is by design, since this is why they are mainly used (to convert a sequence - like text - into a single encoding - #embedding).

The problem

Suppose you have the input: (w0, w1, w2, ..., wn)

What you normally would do for training, maybe in a naive way, is to #autoregress, which means sending all the tokens of the input into the RNN and compute the loss as the result you get at the very end, then backpropagate through time, for all the steps with their relative partial-losses.

If you are in a #seq2seq model (say in #language_models or #machine_translation), where you want to predict a sequence, derived from the input sequence, doing the above ends you up with the following (logically unrolled) algorithm:

• Forward pass:
  • passing w0 into the RNN model and getting a prediction p0.
    • this makes the RNN pass to a new state s0 to reflect the output you just sent

  • (internally) compute the partial-loss l0: between p0 and the expected answer e0

  • send in the next token w1 into the RNN model and getting a prediction p1

  • (internally) compute the partial-loss l1: between p1 and the expected answer e1

  • .… (repeat n times for all w_i)

• after all these steps, you now have the output prediction (p0, p1, p2, ..n, pn), which you want to train so as to be as close as possible to the target (expected) sequence (t0, t1, t2, ..., tn)

• Backwards pass:
  • backpropagate through time, using each l_i as the loss value for each timestep you’re at

So you have:

• (w0, w1, w2, ..., wn) - inputs
• (p0, p1, p2, ..., pn) - outputs
• (t0, t1, t2, ..., tn) - targets
• (l0, l1, l2, ..., ln) - partial-loss values

In this formulation, notice that p1 is only as good as p0 was, because p1 used the RNN that yielded p0. Since usually, p0 is way off (especially at the beginning of training) then p1, p2 and the following have a increasingly smaller chance to land on the correct outputs (because they depend on the previous erroneous states).

Teacher forcing

To overcome this, you actually need not continue on step i from the intermediary state i-1 (that yields p_i) but from a state that received all the correct inputs, up to the current one. In other words, we need to make p_i dependent on the sequence(t0, t1, t2, ..., t(i-1)) not on (p0, p1, p2, ..., p(i-1)).

Let’s take an example. Suppose we want to predict the next word in the sequence (I, am, new) which is at.

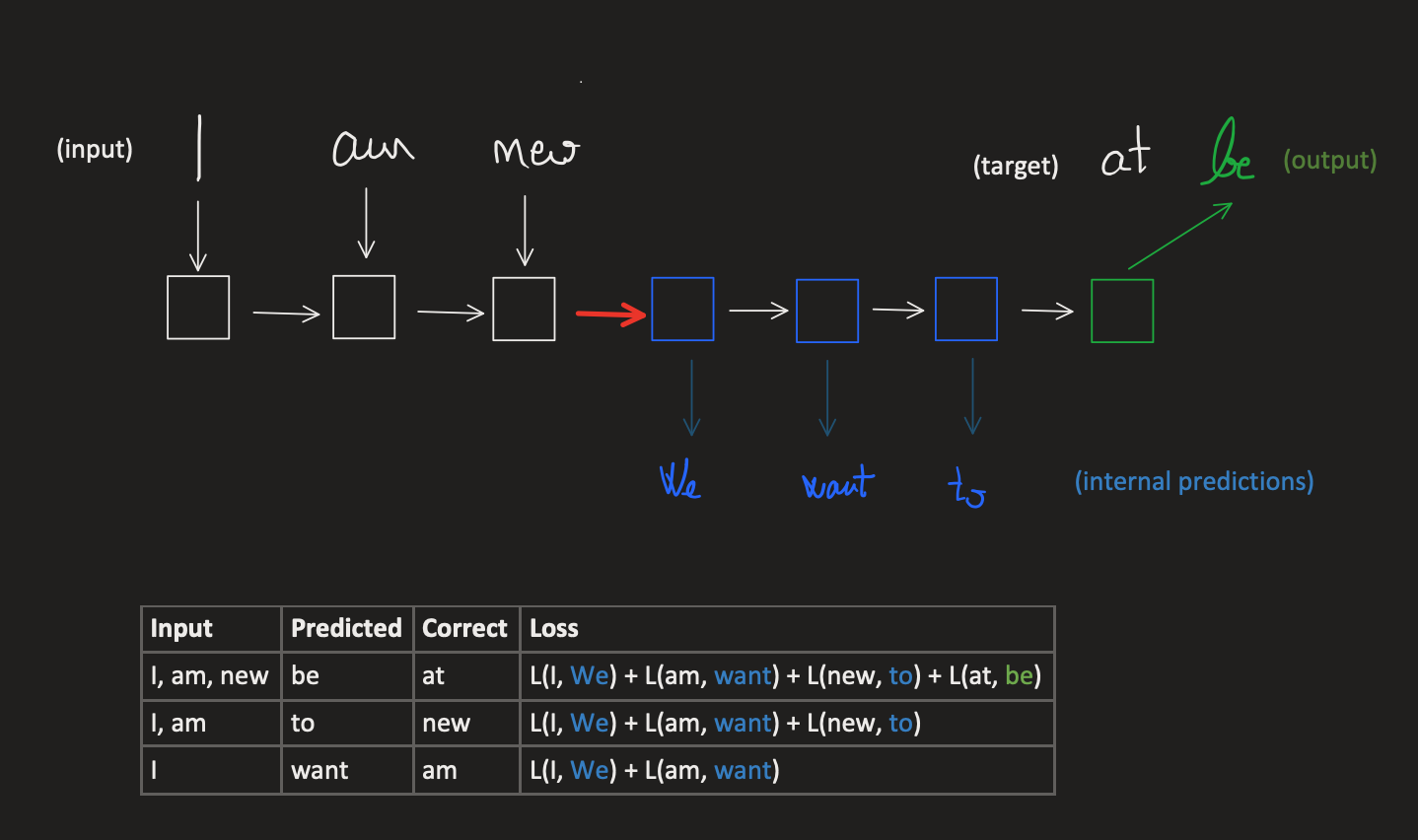
What would normally happen is that you’d pass all the words into the RNN I, am, new and let the RNN build up an internal state representing this sequence, into an internal state (the red arrow above) and and then unroll this hidden state for 3 steps to get the final output.

Internally, at each unrolling step you actually get some intermediary predictions (in blue) and they depend on what the RNN unrolled previously in step (t-1). This means that since We was a wrong prediction, want may be sensible as a next word, given We as a prior, but for the full sequence, it builds up on the previous error. By the time, we get to the output, we have accumulated all the errors of:

• predicting be, which depended on the error of predicting previously both We and want and to
• predicting to which depended on the error of predicting previously both We and want
• predicting want which depended on the error of predicting We

To correct these issues, the backpropagtion step has to compute the loss values as cummulative sums of all the loss values of previous predictions (#”backpropagation through time” #bptt).

Teacher forcing solves this by sending in all the correct predictions as priors, and only deal of forcing (correcting) a single step of the output. It’s as if, we are sending cummulative sequences as inputs, and expect the next token and only backpropagate for that loss value, as you can see in the image bellow.

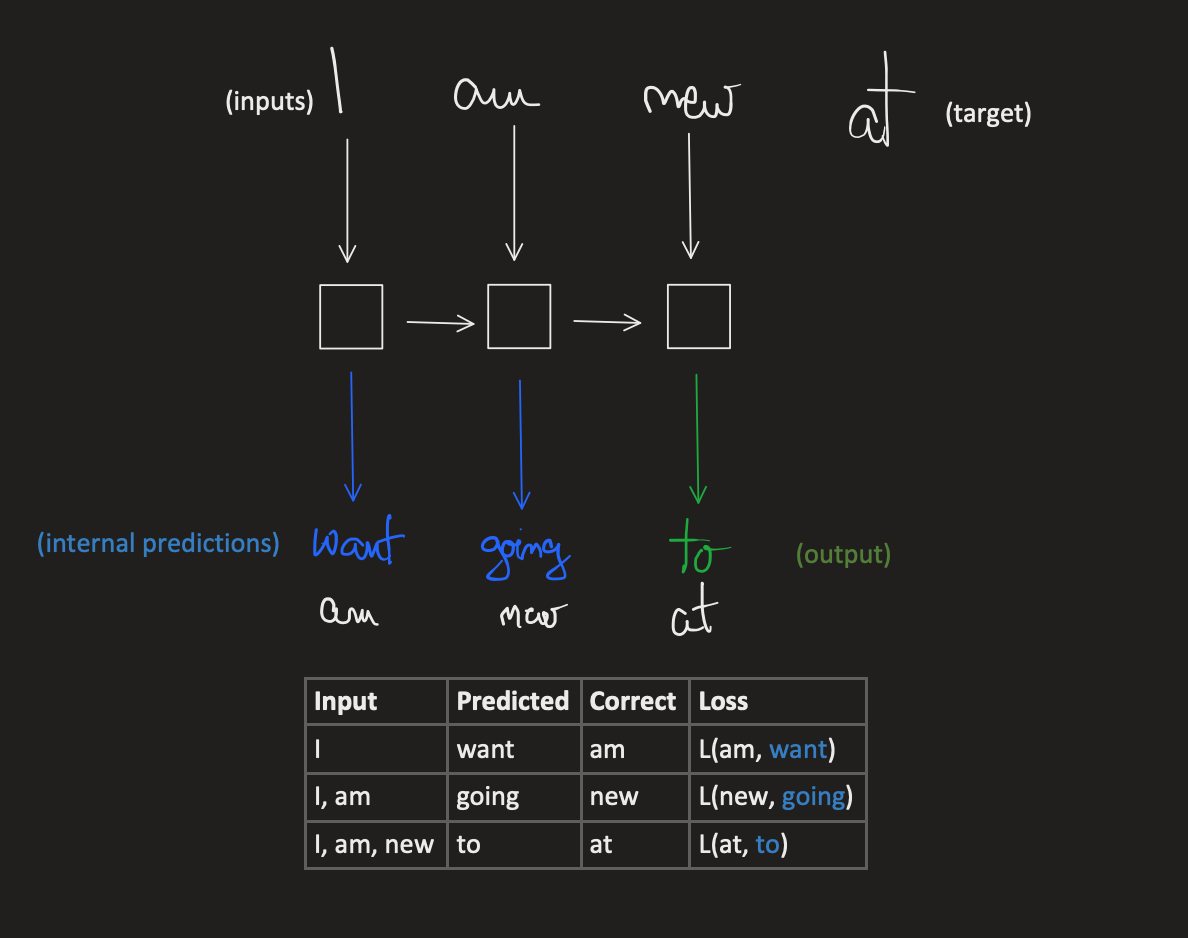
So, we compute the intermediary predictions, we act on their errors (through backpropagation) but only once, since from that point forward we’ll make next tokens depend on the correct previous tokens.

This speeds up training because now we have a linear training schedule, one word at a time.

Basically, if we have a sequence ['I', 'am', 'new'] with should predict at then we need to train the network with the following batch:

• ['I'] -> 'am'
• ['I', 'am'] -> 'new'
• ['I', 'am', 'new'] -> 'at'

This is sometimes also called sequence learning

Credits for this image

See also:

• Teacher forcing used in a machine translation tutorial
• Other teacher forcing explanations